When I was in high school, polar curve is one of my favorite math subject. So I decided to use some concepts from the polar curve to finish this project. I will do the project based on three polar curves: spiral curve, rose curve, and heart shape curve. The major philosophy behind this is to define R and theta, then find the x y value based on them. In order to make things more interesting, some of the z values are the function of x and y.
The first curve I tried is the spiral curve, r = theta; this one is easy:


To add some flavors to this simple shape, I make the z value as a function of x and y; to be specifically z = Zmax*(1-(x^2+y^2)/(x_max^2+y_max^2)); this can add a weight to the z value, when x and y values are small, z will be larger/taller.
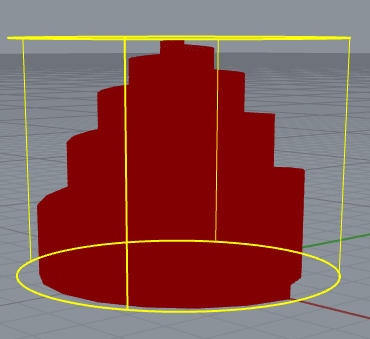


This is harder to print out, I tried different parameters such as the extruder width and speed. But the result is still not ideal. I will try this again using broader width.
The next curve I tried is the heart curve, but I tried the polar curve of r = a+bcos(theta); but no matter how I tune the a and b values, the shape is not exactly what we need.
So I turned into parametric equations to draw a better heart shape curve. Like this one:

What I tried is to use the neural network method to try different combinations of the trigonometric function order, phase, and magnitude. It will take a long time if we use brutal force approach. I manually developed a neural network for it. The learning rate of the neural network is set to 1 since I want all of these parameters to be integers. The neural network method can stop within 1 seconds by setting the mean square error tolerance threshold to 0.01. The fit I find is x = 16sin(theta)^3; y=13cos(theta) – 5cos(2theta)-2cos(3theta)-cos(4theta); and here is the result:


Last curve is rose curve: r = 35cos(theta); the center is the most tricky part since the nozzle will path the center point for multiple times. This will cause a hump forming in the center point. So what I do is adding a if statement logic, such that when x^2+y^2 is small(near center point), I will set z value aliitle bit smaller. In this way the hump will be gone.


The code I used can be find here:
https://handandmachine.org/classes/computational_fabrication/wp-content/uploads/2023/10/p3.gh
Hello,
Very nice works. I am wondering are there other ways to curve the petel?
Jingbo
Hello Lin, I found it so funny we did almost exact objects. You obviously knew way more of the math behind it than me. I all I had done was just look up mathematical designs. Great Work!
Hello Lin, your heart shape using the neural network to fine tune the values to use turned out incredible. I’m impressed that you developed a network in the time we had for this project.