by Daniel Morales-Garcia
Part 1: Turtle Geometry
1.) polygonHalt()
Looking at the ‘polygonHalt’ function, it moves the turtle forward a certain distance (‘size’) and then turns it by a certain angle (‘angle’). It continues doing this until the total rotation is a multiple of 360 degrees, at which point the turtle stops.

To solve the given problems, I started determining the number of segments that the turtle will make, and the length of each segment.
- The total rotation before halting is the smallest multiple of the ‘angle’ that is greater than or equal to 360. If ‘angle’ divides 360 evenly, then the total rotation is 360. Otherwise, it will be some multiple of the angle greater than 360. The number of segments n is the total rotation divided by the ‘angle’.
- Since we are considering a circle approximation, the total circumference C is n × size.
1.a) polygonHalt(1, 1)
The turtle moves forward by 1 unit and turns 1 degree, repeating this until it completes a full circle. Therefore, the turtle will make 360 segments of 1 unit each.
So, the total circumference C = 360 × 1 = 360 units.
If I plug in 360 into the equation for radius if a circle, I get the following:

The radius of the circle is approximately 57.3 units.
1.b) polygonHalt(n, n)
The curvature remains constant since the ‘angle’ is always the ‘size’ for each function call. So for any function call polygonHalt(n, n):
The circumference C = 360 × n.
Given that the curvature remains the same, the radius r for each of these circles will be the same as in part a.
2.) Theorem Application
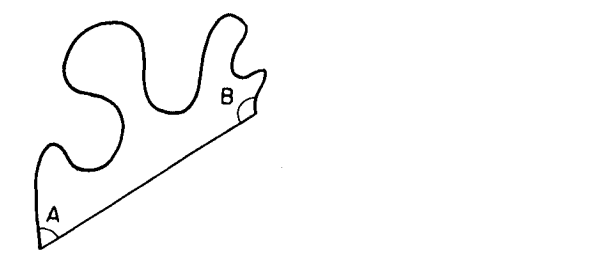
Imagine a gentle arcing path that for simplicity’s sake does not cross itself. Think of it as half of a perfect circle or a section of a curve that one might find in nature. Now, connect the two endpoints of this arc with a straight line, as visible below in Figure 1.
The Simple-Closed-Path Theorem:
As mentioned in the reading from the Introduction to Turtle Geometry, the Simple-Closed-Path Theorem asserts that the total turning in any simple closed path is an integer multiple of 360°. It’s a fascinating idea that speaks to the rotation and turning one experiences as they traverse a closed path.
Relating the Arc to the Theorem:
Now, if we think of our arc and the straight line as forming a simple closed path, the theorem can be applied. Given that the arc does not intersect with the straight line anywhere except at the endpoints, we can see that our arc combined with the straight line forms a simple shape similar to a ‘D’.
Given the theorem, the exterior angles of our ‘D‘ shaped figure would sum up to 360°. Since the exterior angle at any point on a straight line is 180°, the total turning over the arc would be: 360° – 180° = 180°.
So, A + B = 180°.
Part 2: L-Systems
L-System 1: Unidentified Tree
The following tree might strike a chord of familiarity with many, as it stands right outside UNM’s Mechanical Engineering Building. Although unidentified, the tree’s distinct vase-like shape and cordate green leaves does not go unappreciated.

Crafting the L-System for the unidentified tree outside the Mechanical Engineering building was a mix of trial, error, and some luck when it came to the randomization of the tree. Capturing its vase shape while maintaining a rounded shape with erratic branches and leaves was not a quick task. I wanted to showcase the tree’s intricate branches, which meant being strategic with the leaf placement/size. Too many leaves, and the branches would disappear. Too few, and the tree looked bare. I eventually came up with the following L-System drawing that I was satisfied with.


L-System 2: Dieffenbachia (Dumb Cane)
Dumb Cane (Dieffenbachia), is a popular houseplant that I came across at my workplace. With its characteristic broad leaves marked with splashes of white tint, it’s not just a vibrant decoration but also an exciting plant for my L-System model. The plant’s vertical growth with intermittent branching and alternating droopy leaf arrangement offered insights into crafting a model that represents its stature and aesthetic.

Working out the L-System for the Dumb Cane was tougher than expected. The symmetry of the plant, especially how the leaves angled became my biggest challenge. I spent some time tweaking the rotation angles, aiming to capture that natural bend and droop the closer leaves have, as if they’re leaning forward.

Dumb Cane L-System Pattern

L-System 3: Unidentified Bush
Right outside my house I encountered this beautiful unidentified bush. While there’s nothing flashy about this bush, the symmetry captivated me to create an L-System for this plant.

Developing the L-System was straightforward, but did present some challenges. My initial challenge was striking the right balance with the leaf size. I wanted to show off some of the branches underneath, but every time I got that right, the bush looked way too hollow. It was like trying to find the sweet spot between a full-bodied bush and a skeletal frame. It took quite a few tweaks and lots of back and forths, but eventually, I managed to get a representation that did justice to its natural blend of leaves and branches. The process was both frustrating and rewarding.
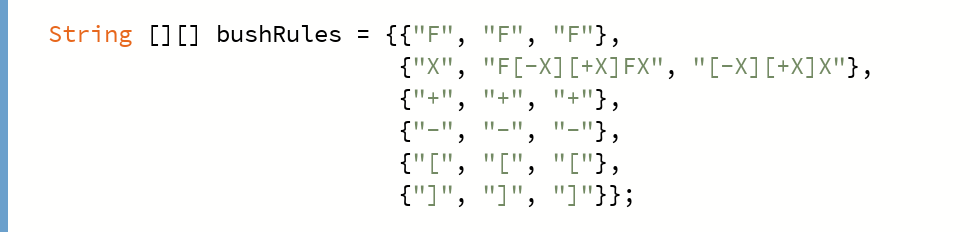
MysteryBush L-System Pattern

Fabricated Design on Clothing
I chose to go with the tree for my fabrication design. I printed on an old T-shirt that I wear around the house. One of the primary issues I grappled with was scaling. I found that I wanted the tree to look like a small logo on the T-shirt. It took me a few tries printing before I was able to find what I think is the perfect size, but I am content with the result!



Code
Sources
Petruzzello, Melissa. (2023, February 10). Dumb Cane. Britannica. https://www.britannica.com/plant/dumb-cane/additional-info#history