Small Assignment 2 – Connor Frost

Hello!

I have divided up the response into sections for each part of the homework. Please find my code attached to this post.

Thank you

Problem 1

I decided to draw the polar plot by splitting up the drawing of the circular rings indicating the radius and the drawing of the lines indicating the angle from the origin. The drawing of the circles is simply using the ellipse function to draw repeating circles for a finite amount. The drawing of the angled lines take inspiration from some of the exercises in class which drew a line with respect to the angle and the radius for drawing every line up to 360 degrees. I added a little bit of color to remind me of graphing paper.

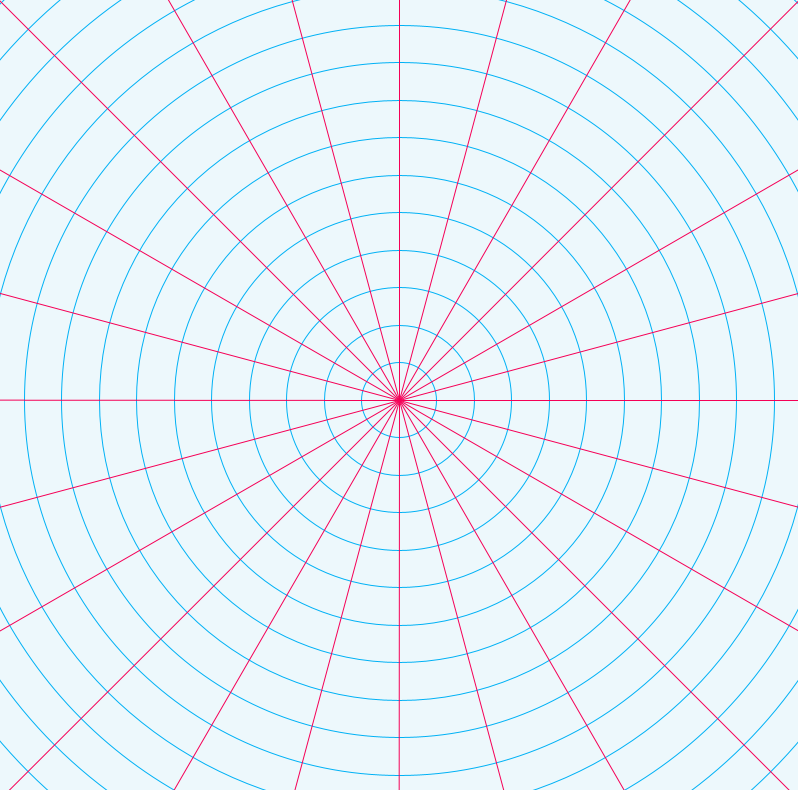
EDIT / UPDATE: It appears I mixed up a polar plot with a polar coordinate system.

Problem 2

To draw a centered circle, there were primarily two tasks for me in solving this: The first being getting to a place that you can start to even draw a circle, and the second being the actual drawing of the circle. I used the penUp procedure and go the radius distance away from the center. After leaving the center and getting to an edge, I used the function that we worked on in class that could plot a circle (primarily, the polygon function with size 1, and an angle increment every so often). By using a bit of math, I determined we can modify the size of the small 1 degree increments to get a custom-sized circle with respect to the specified radius. Here is the result.

Problem 3

To solve the pedals, I deconstructed the problem into the following solvable components.

• Drawing the angled line out of the middle for a pedal. This was solved by turning left at an angle/2 where angle is calculated by the total number of sides.
• Drawing the half-circle. This was probably the trickiest part as I needed to calculate the base of the isosceles triangle from the sides and the angle. To do this, I used the law of cosines to get length of the other side and then divided by 1/2 to calculate the radius of the circle to draw. The half-circle is easy to draw given the code used in problem 2. There were a few angle adjustments needed to draw the top of the pedal in a non-continuous manner that made returning to the midpoint easier.
• Drawing the return line for the pedal. This is simply calculating the remaining angle to close the shape.
• Drawing the inside circle is simple as we are allowed to use the ellipse function which is pretty self-explanatory.

By looping the calculations of the pedals, I was able to abstract out the creation of any flower to a simple function. The results is given in the images below:

Problem 4

I decided to adopt some of the code from class for my first turtle procedure. This is expanding on some of the code we used in class.

This is the revolving spiral example abstracted and expanded upon by introducing the size of the strokes as a variable in the drawing. By increasing the size of the stroke, the spirals get larger and coalesce into a nice image.

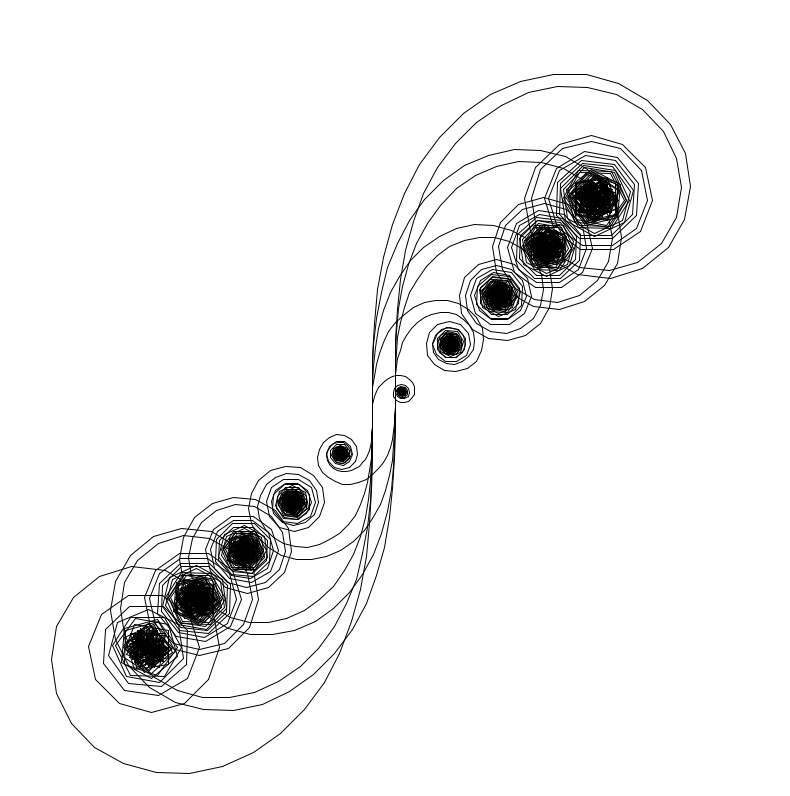
I personally liked this image because of the structure within the chaos. It starts with a simple square spiral and as the angle increases, more complex shapes form. Star-like shapes form to create the ring but you can still observe general shapes.

Drawing circles while on a random walk produces very interesting pictures. Using turtle makes this easy to work on as the position is completely relative.

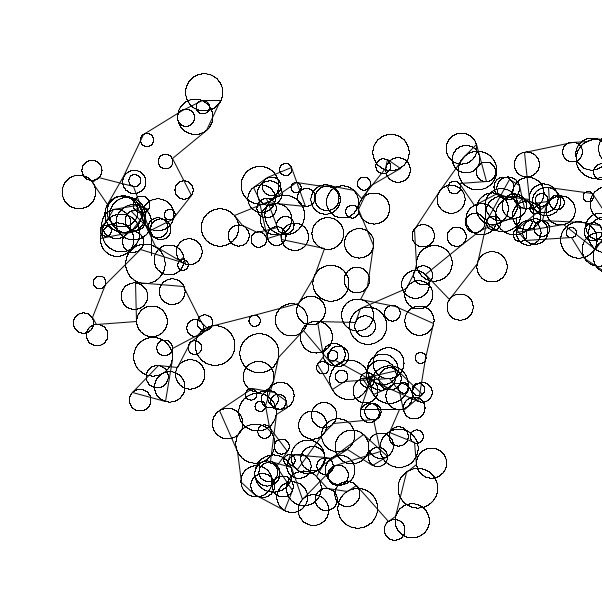
Link to code: https://handandmachine.org/classes/computational_fabrication/wp-content/uploads/2022/02/ConnorFrostSA2.zip